
Bất đẳng thức Cosin là bất đẳng thức được áp dụng và sử dụng rất nhiều. Bắt đầu từ lớp 8 khi tiếp xúc với bất đẳng thức rồi bất đẳng thức Cosin ( Caushy ) cho đến lớp 12, đây là công thức được sử dụng rất nhiều
Vì thế hãy theo dõi những nội dung dưới đây để nắm bắt tốt các kiến thức hữu ích nhé !
Tham khảo bài viết khác:
Bất đẳng thức Cosin là gì ?
Tóm tắt nội dung
– Bất đẳng thức Côsi là một trong những bất đẳng thức cổ điển. Tên chính xác là bất đẳng thức giữa trung bình cộng và trung bình nhân, nhiều người gọi là bất đẳng thức AM – GM (AM là viết tắt của Arithmetic mean và GM là viết tắt của Geometric mean).
– Do nhà toán học người Pháp Augustin – Louis Cauchy (1789 – 1857), người đã đưa ra một cách chừng mình đặc sắc nên nhiều người hay gọi là bất đẳng thức Cauchy.

Bất đẳng thức Cosin cho 2 số
– Công thức được áp dụng cho 2 số không âm
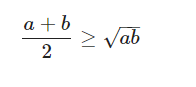
Bất đẳng thức Cosin cho 3 số
– Công thức được áp dụng cho 3 số không âm
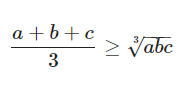
===> Công thức tổng quát áp dụng cho n số không âm
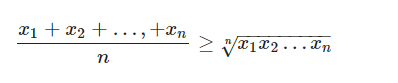
Chứng minh bất đẳng thức Cosin đúng với 2 thực số không âm
– Rõ ràng với a = 0 và b = 0 thì bất đẳng thức luôn đúng (1). Ta chỉ cần chứng minh bất đẳng thức luôn đúng với 2 số a, b dương.

Ví dụ minh họa

Cám ơn bạn đã theo dõi bài viết của chúng tôi, hẹn gặp lại các bạn ở những bài viết khác !





