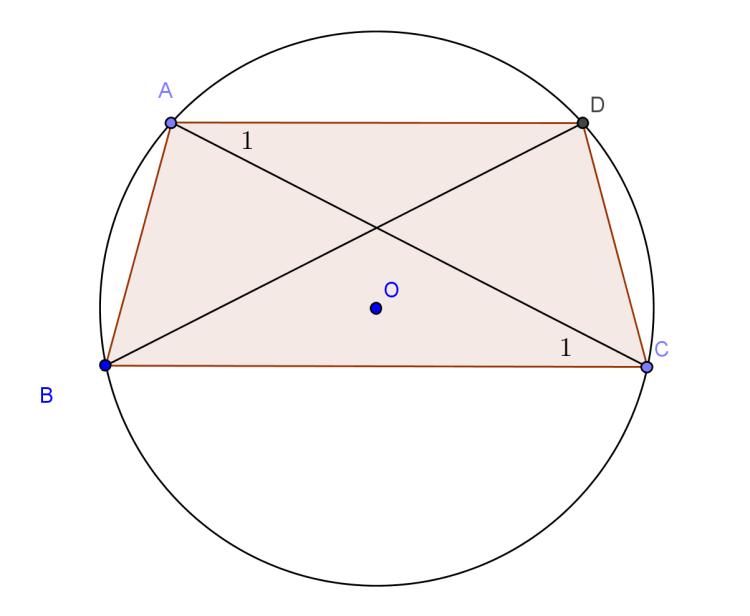
Hình thang cân nội tiếp đường tròn trong bài hình thang cân cho chúng ta những kiến thức hay ho bổ ích nào ? Cùng Đồng Hành Cho Cuộc Sống Tốt Đẹp đi tìm hiểu và chứng minh trong bài viết này nhé !
Tham khảo bài viết khác:
Định Nghĩa Hình Thang Cân Là Gì ?
Tóm tắt nội dung
– Hình thang là một tứ giác lồi có 2 cạnh đối song song. Hai cạnh này được gọi là hai cạnh đáy của hình thang. Hai cạnh còn lại là hai cạnh bên,
Các trường hợp đặc biệt của hình thang:
- Hình thang vuông: Hình thang có 1 góc vuông được gọi là hình thang vuông
- Hình thang cân: Hình thang có 2 góc kề một cạnh đáy bằng nhau là hình thang cân.
- Hình thang vuông cân: Là hình thang vừa vuông vừa cân và còn được gọi là hình chữ nhật.
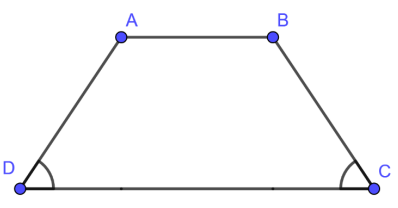
Hình minh họa: Hình thang cân
– Tính chất về góc: Hai góc kề một cạnh bên của hình thang có tổng bằng 1800 ( nằm ở vị trí trong cùng phía của hai đoạn thẳng song song là hai cạnh đáy).
– Ví dụ hình thang ABCD (AB // CD):
- AB và CD gọi là các cạnh đáy ( hoặc đáy). AB là đáy nhỏ, CD là đáy lớn.
- AD và BC gọi là các cạnh bên.
- Gọi AH là đường cao kẻ từ A đến CD. Khi đó, AH là đường cao của hình thang.
Bài Tập Minh Họa Chứng Minh Hình Thang Cân
Ví dụ: Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông ( hình bên dưới ), Tứ giác nào là hình thang cân ? Vì sao ?
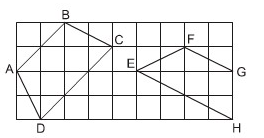
Hướng dẫn giải:
Để nhận biết được tứ giác nào là hình thang cân thì phải dùng tính chất: “Hình thang cân có hai cạnh bên bằng nhau”.
Tứ giác ABCD là hình thang cân vì AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Hình Thang Cân Nội Tiếp Đường Tròn
– Tính chất 4 ở bài tính chất hình thang cân đã nói rằng ” Hình thang cân luôn nội tiếp được trong một đường tròn”. Và chiều ngược lại cũng đúng, tức: Một hình thang nội tiếp đường tròn là hình thang cân.

Chứng minh hình thang cân nội tiếp hình tròn
![]()
– Hoặc cách khác như:
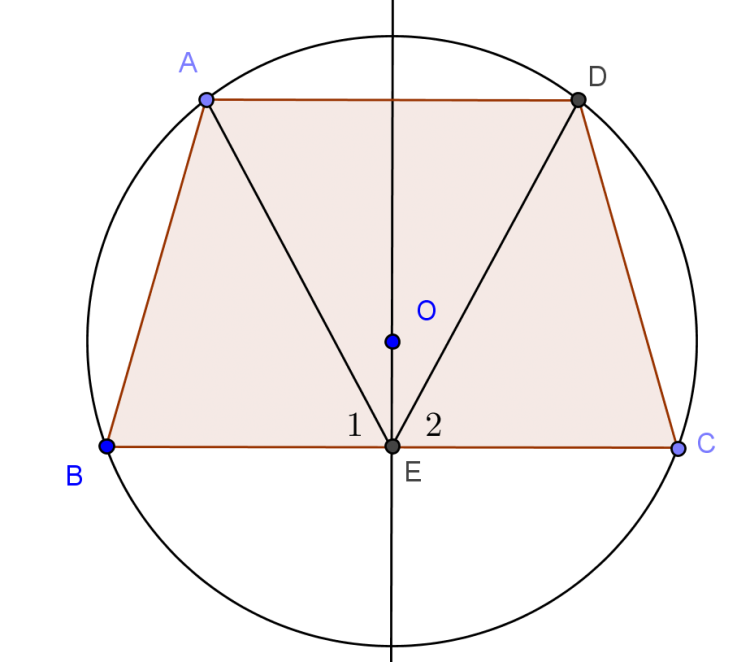
![]()
Với nội dung Hình thang cân nội tiếp đường tròn trong bài viết trên hy vọng sẽ có ích với những bạn đang cần nhé ! Cám ơn các bạn đã theo dõi bài viết này !





