Các tập hợp số trong toán học sẽ cho bạn biết được từng loại với các thông tin đầy đủ. Hơn hết chính là mối quan hệ của các tập hợp đó trong Toán Học.
Với những nội dung dưới bài viết này, chắc chắn sẽ cho bạn thêm nhiều nội dung hữu ích !
Tham khảo bài viết khác:
Lý thuyết các tập hợp số học
Tóm tắt nội dung
1. Tập hợp số tự nhiên, kí hiệu N
N = { 1; 2; 3; 4; 5…….}
2. Tập hợp số nguyên, kí hiệu là Z
Z = { … -3; -2; -1; 0; 1; 2; 3……..}
– Tập hợp số nguyên gồm các phần tử là số tự nhiên và các phần tử đối của các số tự nhiên.
– Tập hợp các số nguyên dương kí hiệu là N∗
3. Tập hợp số hữu tỉ, kí hiệu là Q
Q = { a/b / a, b ∈ Z, b ≠ 0 }
– Mỗi số hữu tỉ có thể biểu diễn bằng một số thập phân hữu hạn hoặc vô hạn tuần hoàn.
4. Tập hợp số thực, kí hiệu là R
– Một số được biểu diễn bằng một số thập phân vô hạn không tuần hoàn được gọi là một số vô tỉ. Tập hợp các số vô tỉ kí hiệu là I
– Tập hợp số thực gồm các số hữu tỉ và các số vô tỉ:
R = Q ∪ I
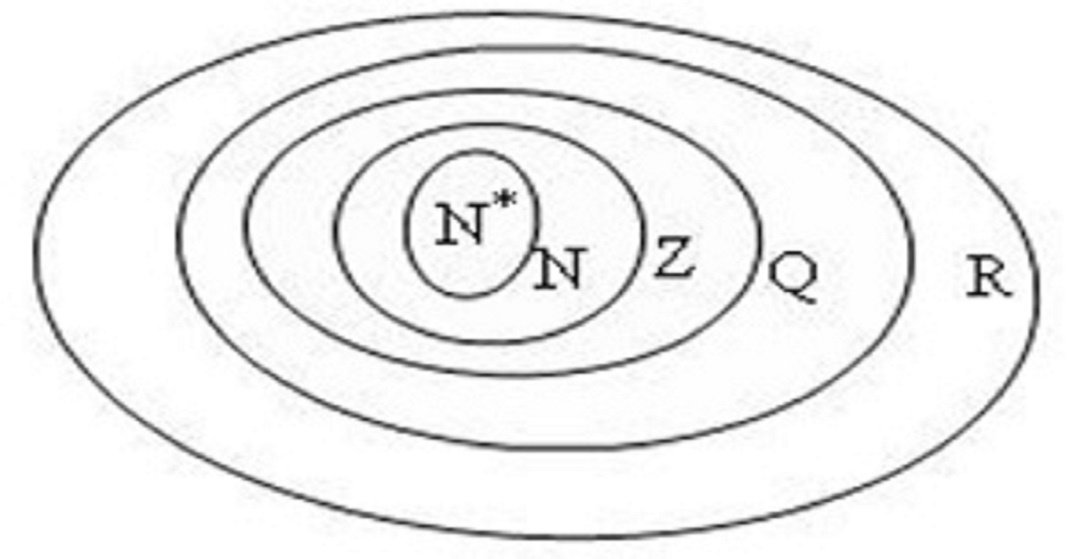
5. Mối quan hệ các tập hợp số
+) Ta có : R = Q ∪ I.
+) Tập N ; Z ; Q ; R.
==> Khi đó quan hệ bao hàm giữa các tập hợp số là : N ⊂ Z ⊂ Q ⊂ R
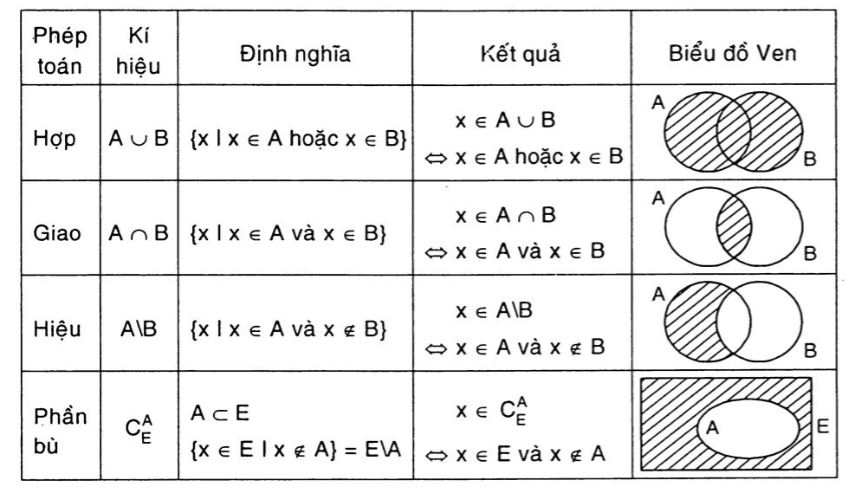
Các phép toán trong tập hợp của toán học
Với các phép toán trong tập hợp số học dưới đây, bạn sẽ biết được mối quan hệ của chúng.
Bài tập về các tập hợp số học trong Toán
Bài 1: Chọn câu trả lời đúng trong các câu sau:
a) [a;b] ⊂ (a;b]
b) [a;b) ⊂ (a;b]
c) [a;b] ⊂ (a;b)
d) (a;b], [a;b) đều là tập con của [a;b]
Hướng Dẫn Giải:
Chọn đáp án D. Vì [a;b] là tập lớn nhất trong 4 tập hợp:
Bài 2: Xác định mỗi tập hợp sau:
a) [-2;4)∪(0;5]
b) (-1;6]∩[1;7)
c) (-∞;7)\(1;9)
Hướng Dẫn Giải:
a) [-2;4)∪(0;5]=[-2;5]
b) (-1;6]∩[1;7)=[1;6]
c) (-∞;7)\(1;9)=(-∞;1]
Đây là dạng toán thường gặp nhất, để giải nhanh dạng toán này ta cần vẽ các tập hợp lên trục số thực trước, phần lấy ta sẽ giữa nguyên còn phần không lấy ta sẽ gạch bỏ đi. Sau đó việc lấy giao, hợp hay hiệu sẽ dễ dàng hơn.
Bài 3: Xác định mỗi tập hợp sau
a) (-∞;1]∩(1;2)
b) (-5;7]∩[3;8)
c) (-5;2)∪[-1;4]
d) (-3;2)\[0;3]
e) R\(-∞;9)
Hướng Dẫn Giải:
a) (-∞;1]∩(1;2) ≠ ∅
b) (-5;7]∩[3;8) = [3;7)
c) (-5;2)∪[-1;4] = (-1;2)
d) (-3;2)\[0;3] = (-3;0]
e) R\(-∞;9) = [9;+∞)
Cám ơn bạn đã theo dõi bài viết nói về các tập hợp số trong Toán Học cũng như mối quan hệ của chúng. Hy vọng bài viết dưới đây sẽ cho bạn những nội dung hữu ích nhất nhé !





