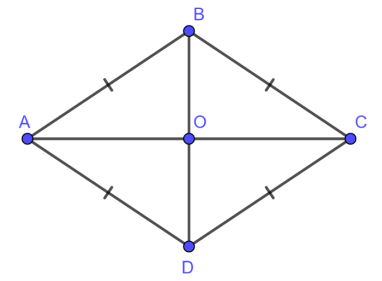
Dấu hiệu nhận biết hình thoi kèm theo là những bài chứng minh từng dấu hiệu nhận biết của hình thoi giúp bạn giải quyết nhanh chóng các vấn đề của mình
Cùng chúng tôi theo dõi ngay những nội dung dưới bài viết này nhé !
Tham khảo bài viết khác:
Dấu hiệu nhận biết hình thoi đầy đủ, chi tiết
Tóm tắt nội dung
– Hình thoi có 4 dấu hiệu nhận biết, như sau:
- Tứ giác có 4 cạnh bằng nhau
- Hình bình hành cá hai cạnh kề bằng nhau
- Hình bình hành có hai đường chéo vuông góc nhau
- Hình bình hành có 1 đường chéo là đường phân giác của 1 góc.
==> Bên cạnh đó, hình thoi cũng là một hình bình hành đặc biệt. Nếu tứ giác đã biết là một hình bình hành và có những đặc điểm dưới đây thì tứ giác đó là hình thoi:
- Có hai cạnh kề bằng nhau là hình thoi.
- Có hai đường chéo vuông góc với nhau
- Có một đường chéo là đường phân giác của một góc

Chứng minh các dấu hiệu nhận biết của hình thoi
1. Chứng minh dấu hiệu : Tứ giác có bốn cạnh bằng nhau
Ví dụ minh họa 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.
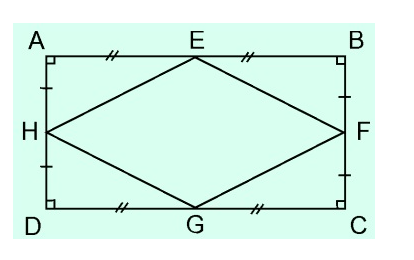
Hướng dẫn chứng minh:
Xét ΔABD có E và H lần lượt là trung điểm của AB và AD
⇒ EH là đường trung bình của ΔABD
⇒ EH = 1/2 BD (1)
Chứng minh tương tự ta có: EF = 1/2 AC; FG = 1/2 BD; HG = 1/2 AC (2)
Vì ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2) và (3), ta suy ra EH = EF = HG = GF
⇒ Tứ giác EFGH là hình thoi do có bốn cạnh bằng nhau.
2. Chứng minh dấu hiệu : Tứ giác có 2 đường chéo là đường trung trực của nhau
Ví dụ minh họa 2: Cho hình bình hành ABCD có AB = AC. Kéo dài trung tuyến AM của ΔABC và lấy ME = MA. Chứng minh tư giác ABEC là hình thoi.
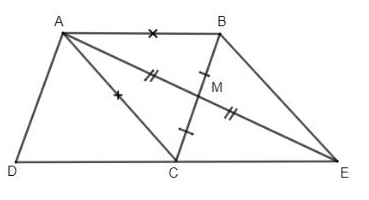
Hướng dẫn chứng minh:
Ta có:
ΔABC cân tại A có trung tuyến AM
⇒ AM là đường trung trực của BC
⇒ Tứ giác ABEC là hình thoi do có 2 đường chéo là đường trung trực của nhau.
3. Chứng minh dấu hiệu : Hình bình hành có hai cạnh kề bằng nhau
Ví dụ minh họa 3: Cho tam giác ABC, lấy các điểm D, E theo thứ tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: IMNK là hình thoi.
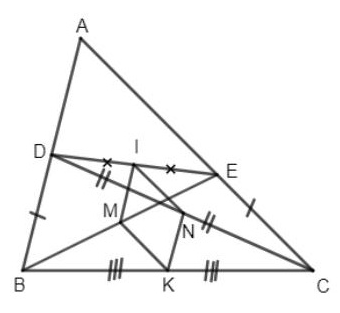
Hướng dẫn chứng minh:
M là trung điểm của BE và I là trung điểm của DE
⇒ MI là đường trung bình của ΔBDE
⇒ MI // BD và MI = 1/2 BD
Chứng minh tương tự, ta có:
NK // BD và NK= 1/2 BD
Do có MI // NK và MI = NK nên tứ giác MINK là hình bình hành (4)
Chứng minh tương tự, ta có: IN là đường trung bình của ΔCDE
⇒ IN = 1/2 CE mà CE = BD (gt) => IN = IM (5)
Từ (4) và (5) ⇒ Tứ giác MINK là hình thoi do là hình bình hành có hai cạnh kề bằng nhau.
4. Chứng minh dấu hiệu : Hình bình hành có hai đường chéo vuông góc
Ví dụ minh họa 4: Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng giao điểm các đường phân giác trong của các tam giác ΔAOB; ΔBOC; ΔCOD và ΔDOA là đỉnh của một hình thoi.
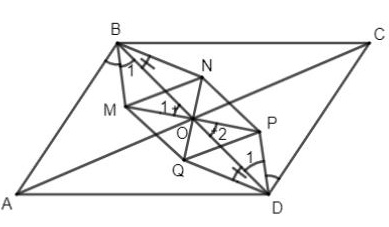
Hướng dẫn chứng minh:
Gọi M, N, P, Q lần lượt là giao điểm các phân giác trong của các tam giác AOB, BOC, COD và DOA.
Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.
Xét ΔBMO và ΔDPO có:
Góc B1 = D1 và Góc O1 = O2 ( đối đỉnh ) và OB = OD (gt)
=> ΔBMO = ΔDPO (g. c. g)
=> OM = OP và các điểm M, O, P thẳng hàng (6)
Chứng minh tương tự: ON = OQ và N, O, P thẳng hàng (7)
Từ (6) và (7) Suy ra: Tứ giác MNPQ là hình bình hành do các đường chéo cắt nhau tại trung điểm mỗi đường. (8)
Mặt khác OM, ON là hai đường phân giác của hai góc kề bù nên OM ⊥ ON. (9)
Từ (8) và (9) suy ra: MNPQ là hình thoi do là hình bình hành có hai đường chéo vuông góc.
Cám ơn bạn đã theo dõi những nội dung của Đồng Hành Cho Cuộc Sống Tốt Đẹp, hẹn gặp lại bạn ở những bài viết khác !





