Diện tích tam giác vuông là trường hợp đặc biệt trong những công thức tính diện tích tam giác. Nó đặc biệt ở chỗ có những công thức nhanh để tính hay công thức của nó có chút đặc biệt
Điều đặc biệt mà donghanhchocuocsongtotdep.vn nói đến là gì ? Hãy cùng chúng tôi tìm hiểu ngay dưới bài viết dưới đây nhé !
Tham khảo bài viết khác:
Định nghĩa tam giác vuông cân là gì ?
Tóm tắt nội dung

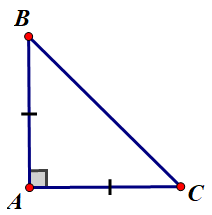
– Tam giác vuông cân vừa là tam giác vuông, vừa là tam giác cân hay nói cách khác tam giác vuông là tam giác có 2 cạnh vuông góc và bằng nhau.
==> Tam giác ABC có AB = AC, AB ⊥ AC thì tam giác ABC vuông cân tại A.
– Tam giác ABC vuông cân tại A có:
- Cạnh AB, AC là cạnh góc vuông ( AB = AC )
- Cạnh BC là cạnh huyền
Công thức tính diện tích tam giác vuông cân
– Phát biểu bằng lời: Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông
– Công thức tính:
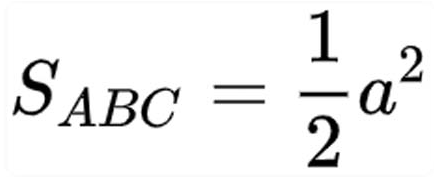
– Trong đó:
- S: Diện tích tam giác
- a: Độ dài của hai cạnh góc vuông
– Ví dụ minh họa : Cho tam giác ABC vuông cân tại A, có AB = AC = 4cm. Tính diện tích tam giác ABC.
Hướng Dẫn Giải:
Do cạnh AB = AC = a = 6cm
Xét tam giác ABC vuông cân tại A, ta có:
S = (a ^ 2): 2 = 16: 2 = 8 cm2
Tính diện tích tam giác vuông khi biết cạnh huyền
+) Cách 1: Sử dụng cách tính nhanh
– Trong tam giác vuông cân, cạnh huyền bằng cạnh góc vuông nhân với căn a.
==> Vì vậy, bạn có thể áp dụng cách này để giải quyết những bài toán. ( Hãy lưu ý đây là tam giác vuông cân nhé, nó chỉ được tính khi 2 cạnh góc vuông bằng nhau )
+) Cách 2: Sử dụng định lý Pitago trong tam giác vuông
– Theo định lý pitago, công thức tính cạnh huyền tam giác vuông cân bằng căn bậc hai của bình phương hai cạnh còn lại
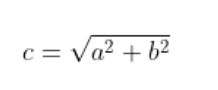
– Trong đó:
- c là cạnh huyền của tam giác vuông cân
- a, b lần lượt là 2 cạnh còn lại
– Bài tập minh họa: Tính diện tích tam giác vuông cân biết cạnh huyền 4cm
Hướng dẫn cách giải:
+) Cách 1:

+) Cách 2:
==> Ta có hệ quả Trong tam giác vuông cân, cạnh huyền bằng cạnh góc vuông nhân với căn 2 ==> cạnh a x căn 2 = 4 ==> a = 4 : căn 2 = 2 căn 2
Hy vọng với những kiến thức mà chúng tôi đem đến cho bạn sẽ là những kiến thức hữu ích giúp các bạn giải quyết những bài toán trên trường nhé !
Cám ơn bạn đã theo dõi, hẹn gặp lại bạn ở những nội dung bài khác !





