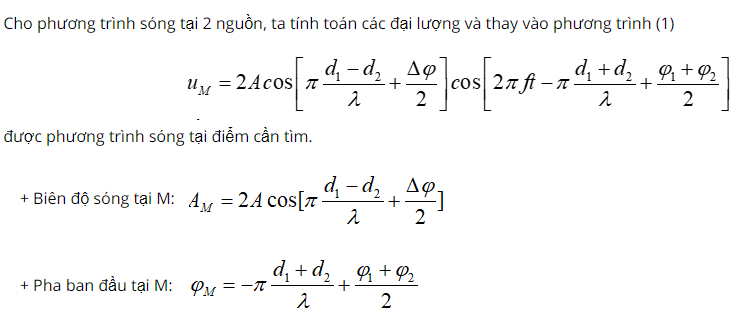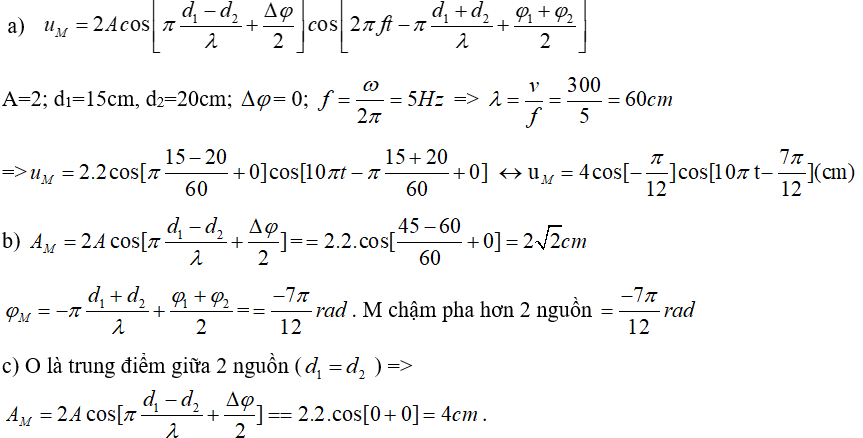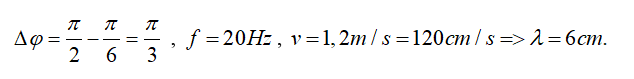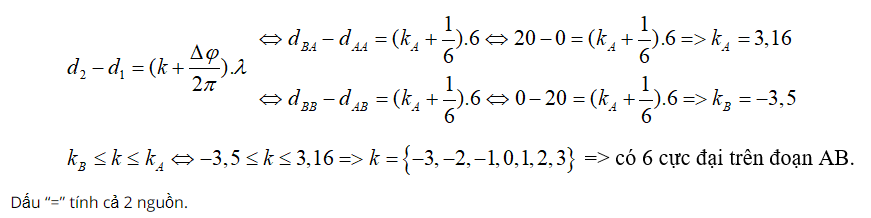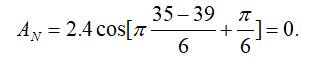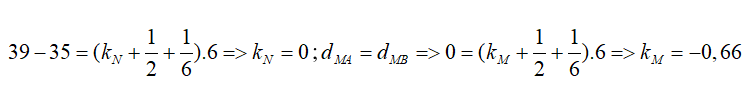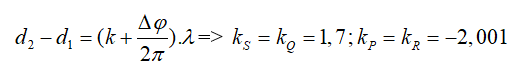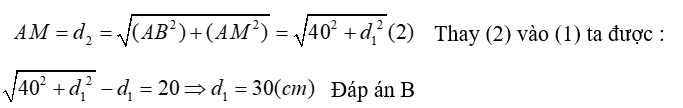
Giao thoa sóng cơ là gì ? Hãy theo dõi bài viết này để hiểu rõ hơn về giao thoa sóng cơ nhé. Những nội dung lý thuyết và bài tập chúng tôi chia sẻ cho bạn trong bài viết này sẽ vô cùng hữu ích đó
Tham khảo bài viết khác:
Giao thoa sóng cơ là gì ?
Tóm tắt nội dung
1. Định nghĩa của giao thoa sóng cơ
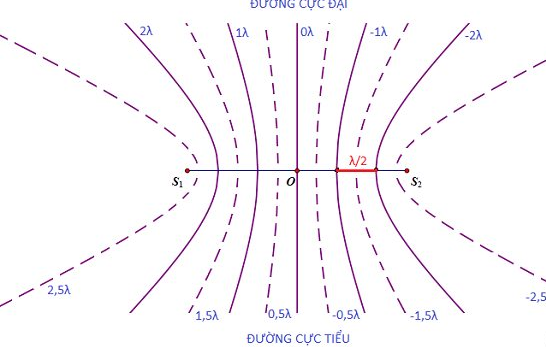
– Giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau tại điểm xác định, luôn luôn hoặc tăng cường nhau, hoặc làm yếu nhau.
==> Giao thoa sóng là sự tổng hợp của hai hay nhiều sóng kết hợp, trên phương truyền sóng những điểm dao động với biên độ max hoặc những điểm dao động với biên độ triệt tiêu.

2. Điều kiện để có hiện tượng giao thoa sóng
– Đó là để có hiện tượng giao thoa sóng là hai sóng phải là hai sóng kết hợp.
– Hai sóng kết hợp là hai sóng có:
- Cùng phương
- Cùng tần số
- Độ lệch pha không đổi theo thời gian
Nguồn kết hợp, sóng kết hợp
– Nguồn kết hợp: Hai nguồn được gọi là nguồn kết hợp khi chúng có cùng phương, cùng tần số, cùng pha hoặc độ lệch pha không đổi theo thời gian.
==> Người ta thường kí hiệu 2 nguồn kết hợp là A và B hoặc S1 và S2. Trong bài này, có khi Ad. dùng AB, đôi khi lại dùng S1S2 .
– Sóng kết hợp: Hai sóng kết hợp là hai sóng xuất phát ra từ nguồn kết hợp.
Chuyên đề bài tập giao thoa sóng có lời giải
==> Các dạng bài tập của giao thoa song có 3 dạng
1. Viết phương trình giao thoa sóng, Tìm biên độ sóng tại 1 điểm
– Phương pháp giải:
– Bài tập minh họa:
Bài tập 1: Trên mặt thoáng của chất lỏng có 2 nguồn kết hợp A,B có phương trình dao động là :uA = uB = 2cos10πt (cm) . Vận tốc truyền sóng là 3m/s.
a) Viết phương trình sóng tại M cách A, B một khoảng lần lượt là d1=15cm, d2=20cm.
b) Tìm biên độ và và pha ban đầu của sóng tại N cách A 45cm, cách B 60cm.
c) Tìm biên độ sóng tại O là trung điểm giữa 2 nguồn.
Hướng dẫn giải
Vậy 2 nguồn cùng pha thì trung điểm giữa 2 nguồn là 1 cực đại giao thoa, Amax = 4cm , dao động với biên độn gấp đôi biên độ của nguồn.
Lưu ý: Làm tương tự như ví dụ c) cho 2 nguồn ngược pha, ta được tại trung điểm là một cực tiểu giao thoa, Amin = 0cm .
2. Cách xác định số điểm dao động với biên độ cực đại, cực tiểu
– Phương pháp giải:
– Bài tập minh họa:
Bài tập 1: Hai nguồn sóng cơ A và B trên mặt chất lỏng cách nhau 20cm dao động theo phương trình uA = 4cos(40πt + π/6) (cm,s) và uB = 4cos(40πt + π/2) (cm,s), lan truyền trong môi trường với tốc độ v = 1,2m/s .
1/ Xét các điểm trên đoạn thẳng nối A với B.
a. Tính khoảng cách giữa hai điểm liên tiếp có biên độ cực đại .
b. Tìm số điểm dao động với biên độ cực đại và cực tiểu giữa 2 nguồn AB.
2/ Tại điểm N trên mặt nước cách A và B lần lượt là d1= 35 cm và d2 = 39 cm dao động có biên độ như thế nào ? Trên đoạn thẳng hạ vuông góc từ N đến đường trung trực của AB có bao nhiêu điểm dao động với biên độ cực tiểu ?
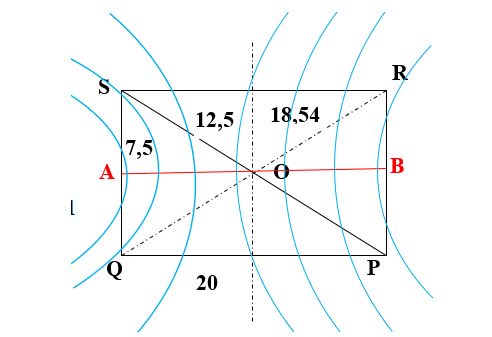
3/ Dựng hình chữ nhật SRPQ, với SR = 15 cm như hình vẽ.
Tìm số cực đại trên đoạn SR, RP, QP, QS, SP, SRPQ.
Hướng dẫn giải:
1/
a) Khoảng cách giữa 2 điểm liên tiếp có biên độ cực đại bằng λ/2 = 3cm .
b) + Số điểm dao động với biên độ cực đại trên đoạn AB, tính cả 2 nguồn:
2/
• Cách 1: Tính biên độ AN thay vào công thức theo dạng 1.
• Cách 2: Giả sử tại N là 1 cực đại, ta có: dNB – dNA = (kN + 1/6).λ ⇒ kN = 0,5 có giá trị bán nguyên nên tại N phải là một cực tiểu bậc 1, có biên độ dao động AN = 0.
Từ N hạ đường vuông góc xuống đường trung trực của AB tại M. Số điểm dao động với biên độ cực tiểu trên đoạn NM là:
⇒ kM ≤ k ≤ kN ⇒ k = {0}, có duy nhất 1 cực tiểu trên đoạn NM và đó là cực tiểu bậc 1 tại N.
3/ Tìm cực đại trên: SR, RP, QP, QS, SP, SRPQ..
Khoảng cách từ các điểm đến 2 nguồn A,B:
Sử dụng điều kiện tìm cực đại với các điểm S, R, P, Q.
+) Trên đoạn SR⇔QP:
-2,001 ≤ k ≤ 1,7 ⇒ k ={-2, -1, 0, 1} ⇒ có 4 cực đại.
+) Trên đoạn SQ: ta tính trên đoạn SA rồi nhân đôi: 1,7≤ k ≤ 3,16 ⇒ k ={2, 3} ⇒ có 2.2=4 cực đại.
+) Trên đoạn RP: ta tính trên đoạn RB rồi nhân đôi: -3,5 ≤ k ≤ -2,001 ⇒ k ={-3} ⇒ có 2.1=2 cực đại.+) Trên Hình chữ nhật SRPQ có số cực đại = 4 + 4 + 4 + 2 = 14 cực đại.
3. Điểm M có tính chất đặc biệt trong Giao thoa sóng
– Phương pháp giải:
Sử dụng các điều kiện cực đại, cực tiểu trong giao thoa sóng và áp dụng kiến thức hình học để giải quyết bài toán dạng này.
– Bài tập minh họa:
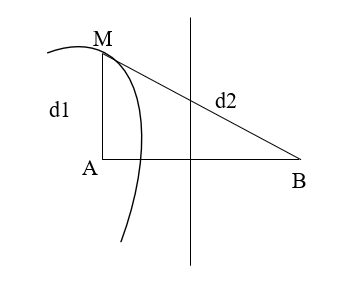
Bài tập 1:Trên bề mặt chất lỏng có hai nguồn kết hợp AB cách nhau 40cm dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số f=10(Hz), vận tốc truyền sóng 2(m/s). Gọi M là một điểm nằm trên đường vuông góc với AB tại đó A dao động với biên độ cực đại. Đoạn AM có giá trị lớn nhất là :
A. 20cm B. 30cm C. 40cm D.50cm
Hướng dẫn giải:
Ta có λ = v/f = 200/10 = 20(cm)
Do M là một cực đại giao thoa nên để đoạn AM có giá trị lớn nhất thì M phải nằm trên vân cực đại bậc 1 như hình vẽ và thỏa mãn :
d2 – d1 = kλ = 1. 20 = 20(cm) (1). ( do lấy k= +1)
Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có :