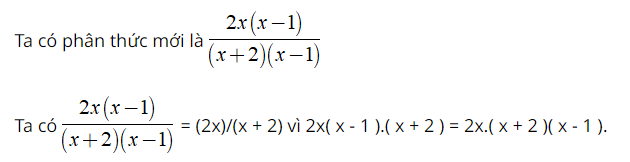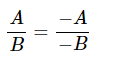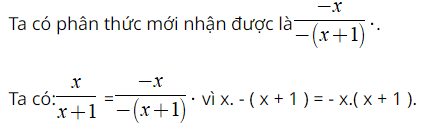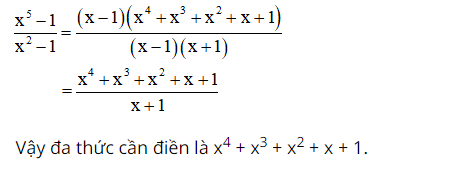Tính chất cơ bản của phân thức đại số gồm những tính chất nào ? Dưới bài viết này chúng tôi sẽ nêu những tính chất cơ bản của các phân thức đại số. Vì thế hãy theo dõi cùng chúng tôi nhé !
Tham khảo bài viết khác:
Tính chất của phân thức đại số
Tóm tắt nội dung
1. Những tính chất cơ bản của phân thức
– Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
– Nếu chia cả tử và mẫu của một đa thức cho một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.
– Ví dụ minh họa: Cho phân thức (2x)/(x + 2). Nhân cả tử và mẫu với đa thức ( x – 1 ), so sánh phân thức nhận được với phân thức đã cho ?
Hướng dẫn giải:

2. Quy tắc đổi dấu
– Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
– Ví dụ minh họa: Ta có phân thức x/ ( x – 1 ) Đổi dấu cả tử và mẫu ta được phân thức mới, so sánh phân thức mới với phân thức đã cho
Hướng dẫn giải:
Bài tập vận dụng tính chất của phân thức
Bài tập 1: Dùng tính chất cơ bản của phân thức để điền một đa thức thích hợp vào chỗ trống
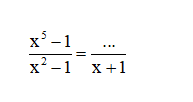
– Hướng dẫn giải:
Ta để ý : x^2 – 1 = (x – 1)(x + 1)
Do đó ta cần chia cả tử và mẫu của phân thức thứ nhất cho x – 1.
Mà ta có :
x ^ 5 – 1 = x ^ 5 – x ^ 4 + x ^ 4 – x ^ 3 + x ^ 3 – x ^ 2 + x ^ 2 – x + x – 1
= x ^ 4 (x – 1) + x ^ 3 (x – 1) + x ^ 2 (x – 1) + x (x – 1) + (x – 1)
= (x – 1) (x4 + x3 + x2 + x + 1)
Do đó :
Cám ơn bạn đã theo dõi bài viết này của chúng tôi, hẹn gặp lại bạn ở bài viết tiếp theo !