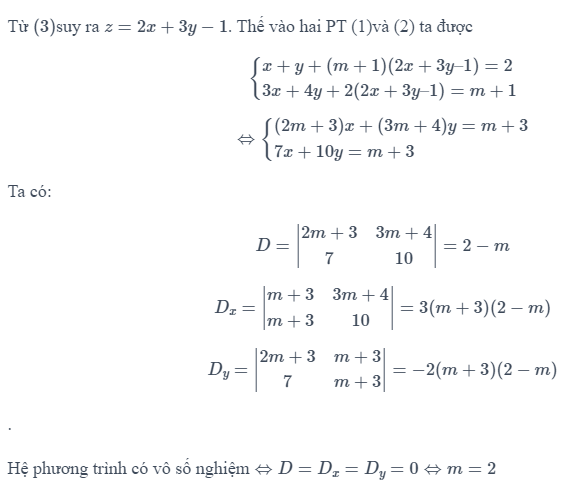Giải phương trình bậc nhất 3 ẩn có phương pháp giải bài tập như thế nào ? Dạng toán này có những dạng toán nào ? Hãy cùng chúng tôi giải đáp câu hỏi dưới bài viết này nhé !
Tham khảo bài viết khác:
Phương trình bậc nhất 3 ẩn
Tóm tắt nội dung
– Định nghĩa :
Phương trình bậc nhất 3 ẩn có dạng tổng quát là: ax + by + cz = d, trong đó x, y, z là ba ẩn, a, b, c, d là các hệ số và a, b, c không đồng thời bằng 0
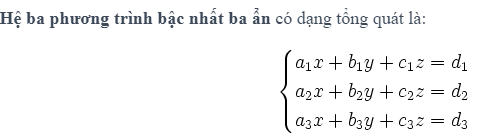
Phương pháp giải phương trình bậc 1 3 ẩn
Phương pháp chung: Dùng phương pháp Gau-xơ khử dần ẩn số để đưa về hệ phương trình dạng tam giác.
a) Phương pháp thế.
- Từ một phương trình của hệ biểu thị một ẩn qua ẩn kia rồi thay vào phương trình còn lại.
b) Phương pháp cộng.
- Biến đôi cho hệ số của một ẩn trong hai phương trình là hai số đối nhau rồi cộng từng vế hai phương trình lại.

Bài tập của phương trình bậc nhất 3 ẩn
Bài tập 1: Giải các phương trình sau:
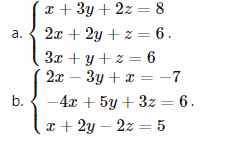
Hướng dẫn giải:
a) Kí hiệu các phương trình của hệ theo thứ tự là (1), (2) và (3), khi đó:
Khử z giữa (1) và (2), ta có: 3x + y = 4. (4)
Khử z giữa (2) và (3), ta có: x – y = 0. (5)
Khử y giữa (4) và (5), ta có: x = 1 => y = 1 => z = 2.
Vậy, hệ phương trình có nghiệm (1; 1; 2).
Hướng dẫn giải:
b. Kí hiệu các phương trình của hệ theo thứ tự là (1), (2) và (3), khi đó:
Khử z giữa (1) và (2), ta được: 10x – 14y = – 27. (4)
Khử z giữa (1) và (3), ta được: 5x – 4y = – 9. (5)
Khử x giữa (4) và (5), ta được: y = 3/2 => x = -3/5 => z = -13/10.
Vậy, nghiệm của hệ phương trình: (-3/5 ; 3/2 ; -13/10).
Bài tập 2: Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau vô nghiệm:
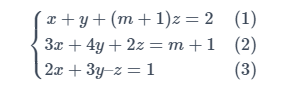
Hướng dẫn giải: