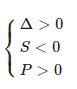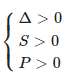
Parabol tiếp xúc với đường thẳng khi nào ? Chúng ta hãy cùng nhau tìm hiểu chi tiết trong bài viết này để thấy được sự tương giao giữa Parabol và đường thẳng thú vị như thế nào nhé !
Tham khảo bài viết khác:
Parabol tiếp xúc với đường thẳng khi nào ?
Tóm tắt nội dung
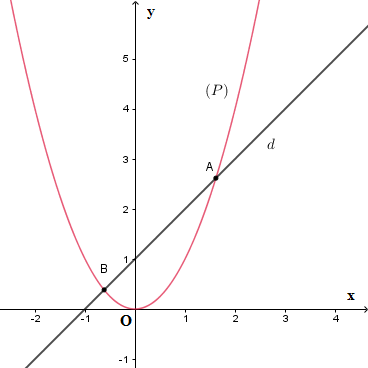
– Sự tương giao giữa đường thẳng d: y = mx + n và parabol (P): y = ax ^2 (a khác 0)
==> Số giao điểm của đường thẳng d và Parabol (P) là số nghiệm của phương trình hoành độ giao điểm
ax^2 = mx + n ⟺ ax^2 – mx – n = 0 (*)
+) Phương trình (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt
+) Phương trình (*) có nghiệm kép thì d tiếp xúc với (P)
+) Phương trình (*) vô nghiệm thì d không cắt (P).

Bài toán tìm m để parabol tiếp xúc với đường thẳng
Xác định tham số m để đường thẳng d : y = mx + n và parabol (P): y = ax^2 ( a ≠ 0 ) cắt nhau tại điểm thỏa mãn điều kiện cho trước .
– Phương pháp giải:
+) Đường thẳng d cắt ( P ) tại hai điểm phân biệt nằm bên trái trục tung ⇔ phương trình (*) có hai nghiệm âm phân biệt
+) Đường thẳng d cắt ( P ) tại hai điểm phân biệt nằm bên phải trục tung ⇔ phương trình (*) có hai nghiệm âm phân biệt
+) Đường thẳng d cắt ( P ) tại hai điểm phân biệt nằm khác phía trục tung ⇔ phương trình (*) có hai nghiệm trái dấu ⇔ a.c < 0
+) Đường thẳng d cắt ( P ) tại hai điểm có tọa độ thỏa mãn biểu thức cho trước (thường biến đổi biểu thức để sử dụng hệ thức Vi-et)
Ví dụ minh họa:

– Hướng dẫn giải:
Cám ơn bạn đã theo dõi bài viết của chúng tôi, hy vọng những nội dung mà chúng tôi chia sẻ về chuyên đề Parabol tiếp xúc với đường thẳng mà mang đến cho bạn những nội dung hữu ích nhất