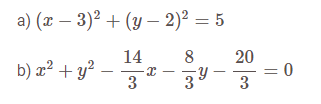
Phương trình của đường tròn được viết bởi công thức nào ? Cùng theo dõi bài viết dưới đây để nắm rõ hơn những nội dung liên quan đến phương trình của đường tròn mà chúng tôi chia sẻ cho bạn nhé !
Tham khảo bài viết khác:
Phương trình tổng quát của đường tròn ?
Tóm tắt nội dung
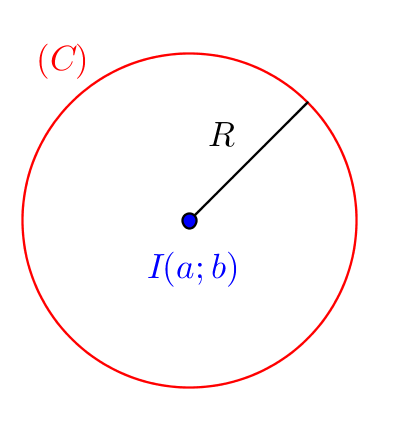
+) Phương trình đường tròn có tâm I (a; b), bán kính R là:
(x – a)^2 + (b – y)^2 = R^2
+) Phương trình đường tròn (x – a)^2 + (b – y)^2 = R^2 có thể viết dưới dạng:
x^2 + y^2 – 2ax – 2by + c = 0
– Trong đó: c = a^2 + b^2 – R^2
– Ngược lại, phương trình x^2 + y^2 – 2ax – 2by + c = 0 là phương trình đường tròn (C) khi và chỉ khi a^2 + b^2 – c > 0.
– Khi đó đường tròn (C) có tâm I (a; b) và bán kính R = √(a2 + b2 – c)

Hướng dẫn cách lập phương trình của đường tròn
Cách 1:
+) Tìm tọa độ tâm I(a; b) của đường tròn (C)
+) Tìm bán kính R của (C)
+) Viết phương trình (C) theo dạng: (x – a)^2 + (y – b)^2 = R2 (1)
Chú ý:
(C) đi qua A, B ⇔ IA^2 = IB^2 = R^2.
(C) đi qua A và tiếp xúc với đường thẳng ∆ tại A ⇔ IA = d(I, ∆).
(C) tiếp xúc với hai đường thẳng ∆1 và ∆2
⇔ d(I, ∆1) = d(I, ∆2) = R
Cách 2:
+) Gọi phương trình đường tròn (C) là x^2 + y^2 – 2ax – 2by + c = 0 (2)
+) Từ điều kiện của đề bài đưa đến hệ phương trình với ba ẩn số là: a, b, c
+) Giải hệ phương trình tìm a, b, c để thay vào (2), ta được phương trình đường tròn (C)
Bài tập lập phương trình tổng quát của đường tròn
Bài 1: Phương trình nào là phương trình đường tròn, hãy tìm bán kính R và tâm I nếu có trong các phương trình sau:
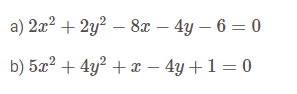
– Hướng dẫn giải:
Bài 2: Lập phương trình đường tròn cho các trường hợp sau đây:
a) Đường kính AB, trong đó A (1;1) và B (5;3)
b) Đi qua A (-1;3); B (3;5); C (4;-2)
– Hướng dẫn giải:
Cám ơn bạn đã theo dõi bài viết của chúng tôi, hy vọng những nội dung chúng tôi chia sẻ đến bạn sẽ giúp ích cho bạn được điều gì đó !