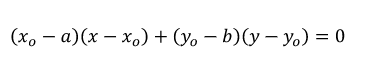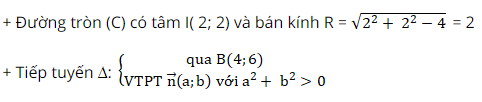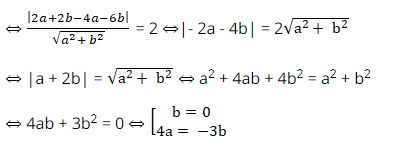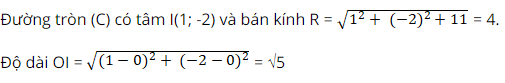
Phương trình tiếp tuyến của hình tròn được viết bởi công thức như thế nào ? Cùng tìm đáp án để có thể viết phương trình nhanh chóng bằng cách tham khảo nội dung dưới bài viết này nhé !
Tham khảo bài viết khác:
Phương trình tiếp tuyến của hình tròn
Tóm tắt nội dung
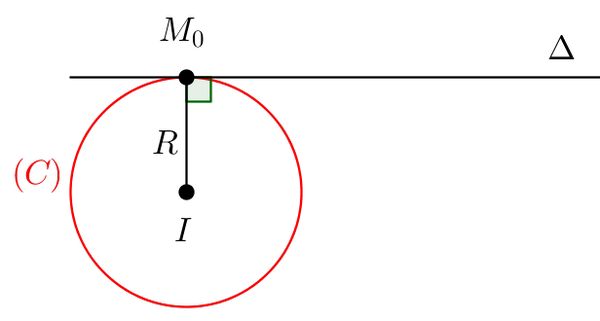
Cho điểm M0 (x0; y0) nằm trên đường tròn (C), tâm I (a; b). Gọi Δ là tiếp tiếp của (C) tại M0.
– Ta có:
+) M0 thuộc Δ và vectơ IM0 = (x0 – a; y0 – b) là vectơ pháp tuyến của Δ.
+) Do đó phương trình của Δ là:
(x0 – a)(x – x0) + (y0 – b) (y – y0) = 0 (1)
Vậy phương trình (1) là phương trình tiếp tuyến của đường tròn (x – a)^2 + (b – y)^2 = R^2 tại điểm M0 (x0; y0) nằm trên đường tròn.

Hướng dẫn cách lập phương trình tiếp tuyến đường tròn
1. Lập phương trình tiếp tuyến tại điểm M0( x0;y0 ) thuộc đường tròn (C)
+) Tìm tọa độ tâm I(a,b) của đường tròn (C)
+) Phương trình tiếp tuyến với (C) tại Mo(xo;yo) có dạng:
2. Lập phương trình tiếp tuyến của ∆ với (C) khi chưa biết tiếp điểm
Bạn hãy dùng điều kiện tiếp xúc với đường tròn (C) tâm I, bán kính R ⇔ d (I, ∆) = R
Bài tập viết phương trình tiếp tuyến cho đường tròn
Bài tập 1: Cho đường tròn (C) : (x – 3)2 + (y – 1)2 = 10. Phương trình tiếp tuyến của (C) tại điểm A( 4; 4) là
- A. x – 3y + 8 = 0.
- B. x + 3y – 16 = 0.
- C. 2x – 3y + 5 = 0 .
- D. x + 3y + 16 = 0.
– Hướng dẫn giải
Đường tròn (C) có tâm I( 3;1). Gọi d là tiếp tuyến của đường tròn (C) tại điểm A; khi đó d và IA vuông góc với nhau.
⇒ IA→ = (1; 3) là vectơ pháp tuyến của d.
Suy ra phương trình d: 1( x – 4) + 3( y – 4 ) = 0
Hay x + 3y – 16 = 0.
==> Đáp án đúng là B
Bài tập 2: Viết phương trình tiếp tuyến ∆ của đường tròn ( C): x2 + y2 – 4x – 4y + 4 = 0, biết tiếp tuyến đi qua điểm B( 4; 6) .
- A. x – 4 = 0 hoặc 3x + 4y – 36 = 0
- B. x – 4 = 0 hoặc y – 6 = 0.
- C. y – 6 = 0 hoặc 3x + 4y – 36 = 0
- D. x – 4 = 0 hoặc 3x – 4y + 12 = 0
– Hướng dẫn giải
⇒ Phương trình ∆: a(x – 4) + b(y – 6) = 0 hay ax + by – 4a – 6b = 0 (*)
+ Do ∆ là tiếp tuyến của đường tròn ( C) nên d(I; ∆) = R
+ Nếu b = 0; chọn a = 1 thay vào (*) ta được ∆: x – 4 = 0.
+ Nếu 4a = – 3b ta chọn a = 3 thì b = -4 thay vào ( *) ta được: 3x – 4y + 12 = 0
Vậy có hai tiếp tuyến thỏa mãn là x – 4 = 0 và 3x – 4y + 12 = 0 .
==> Đáp án đúng là D
Bài tập 3: Có bao nhiêu đường thẳng đi qua gốc tọa độ O và tiếp xúc với đường tròn (C): x^2 + y^2 – 2x + 4y – 11 = 0 ?
– Hướng dẫn giải
⇒ Điểm O nằm trong đường tròn nên không có tiếp tuyến nào của đường tròn kẻ từ O.
Lời kết
Cám ơn bạn đã theo dõi những thông tin mà chúng tôi chia sẻ đến bạn. Hy vọng bài viết này sẽ trở nên hữu ích và giúp được nhiều người giải đáp được các vấn đề !