Phương trình mặt phẳng có rất nhiều nội dung cũng như dạng toán khác nhau đòi hỏi bạn cần nắm bắt thật tốt những lý thuyết cũng như hiểu rõ từng dạng để làm tốt dạng bài này
Hãy theo dõi nội dung dưới đây để chúng tôi có thể chia sẻ cho bạn những nội dung hữu ích nhất nhé !
Tham khảo bài viết khác:
Vecto pháp tuyến là gì ?
Tóm tắt nội dung
– Vectơ n ≠ 0 là vectơ pháp tuyến (VTPT) nếu giá của vecto n vuông góc với mặt phẳng (α)
– Chú ý:
+) Nếu n→ là một VTPT của mặt phẳng (α) thì kn→ cũng là một VTPT của mặt phẳng (α).
+) Một mặt phẳng được xác định duy nhất nếu biết một điểm nó đi qua và một VTPT của nó.
+) Nếu u→, v→ có giá song song hoặc nằm trên mặt phẳng (α) thì n→ = [u→, v→] là một VTPT của (α)

Phương trình của mặt phẳng
1. Phương trình tổng quát của mặt phẳng
– Trong không gian Oxy , mọi mặt phẳng đều có dạng phương trình:
Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
– Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một VTPT là n (A; B; C).
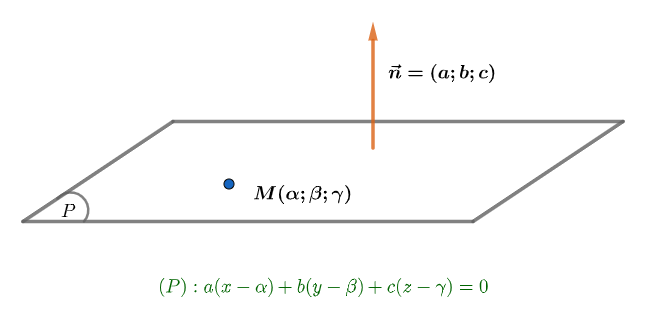
– Phương trình mặt phẳng đi qua điểm M0( x0; y0; z0 ) và nhận vectơ n (A; B; C) khác vecto 0 là VTPT là:
A(x – x0) + B(y – y0) + C(z – z0) = 0
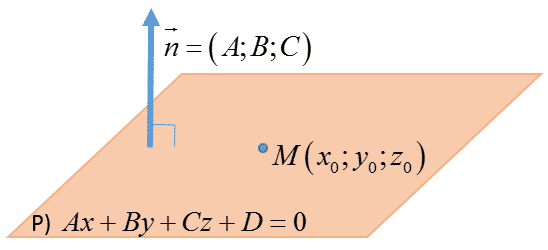
2. Phương trình mặt phẳng theo đoạn chắn
Mặt phẳng đi qua ba điểm M(a ; 0 ; 0), N( 0 ; b ; 0), C(0 ; 0 ; c) ở đó abc ≠ 0 có phương trình :
Phương trình này còn được gọi là phương trình mặt phẳng theo đoạn chắn.
3. Các trường hợp đặc biệt của phương trình mặt phẳng
Xét phương trình mặt phẳng (α): Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
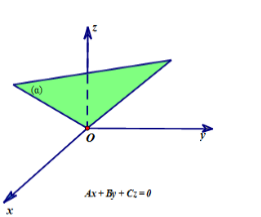
– Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.
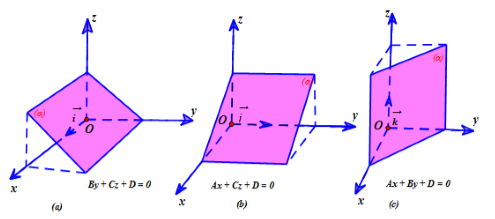
– Nếu A = 0, B ≠ 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Ox.
– Nếu A ≠ 0, B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Oy.
– Nếu A ≠ 0, B ≠ 0, C = 0 thì mặt phẳng (α) song song hoặc chứa trục Oz.
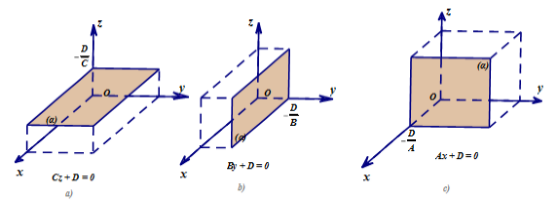
– Nếu A = B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxy).
– Nếu A = C = 0, B ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxz).
– Nếu B = C = 0, A ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oyz).
Một số dạng toán viết phương trình mặt phẳng thường gặp
1. Phương trình mặt phẳng trung trực của đoạn thẳng
– Phương pháp giải:
Giả sử (P) là mặt phẳng trung trực của đoanh AB. Ta xác định yếu tố điểm mà (P) đi qua chính là trung điểm AB. Còn vecto pháp tuyến chính là vecto AB.
2. Phương trình mặt phẳng đi qua 3 điểm cho trước
– Phương pháp giải:
Giả sử mặt phẳng (P) đi qua 3 điểm không thẳng hàng A, B, C. Chúng ta có tới tận 3 yếu tố điểm là điểm A, điểm B, điểm C. Thỏa mái để lựa chọn nhưng ta chỉ chọn 1 điểm thôi nhé. Để tìm yếu tố véc tơ pháp tuyến chúng ta lấy tích có hướng của véc tơ AB và véc tơ AC.
3. Phương trình mặt phẳng đi qua 1 điểm vuông góc với 2 mặt phẳng cho trước
– Phương pháp giải:
Giả sử ta cần viết phương trình mặt (R) đi qua điểm A và vuông góc với (P), (Q). Yếu tố điểm đã có là điểm A. Yếu tố véc tơ pháp tuyến chính là tích có hướng hai véc tơ pháp tuyến của (P) và (Q).
Cám ơn bạn đã theo dõi những thông tin nội dung bài viết của chúng tôi, hy vọng sau bài viết bạn sẽ hiểu hơn về phương trình mặt phẳng trong không gian nhé !