Phương trình tiếp tuyến là một dạng toán rất hay và thú vị. Trong chuyên đề này có rất nhiều dạng toán khác nhau đòi hỏi học sinh cần nắm bắt và hiểu rõ vấn đề
Dưới bài viết này hãy cùng chúng tôi điểm lại những thông tin quan trọng trong chuyền đề về phương trình tiếp tuyến này nhé !
Tham khảo bài viết khác:
Công thức viết phương trình tiếp tuyến
Tóm tắt nội dung
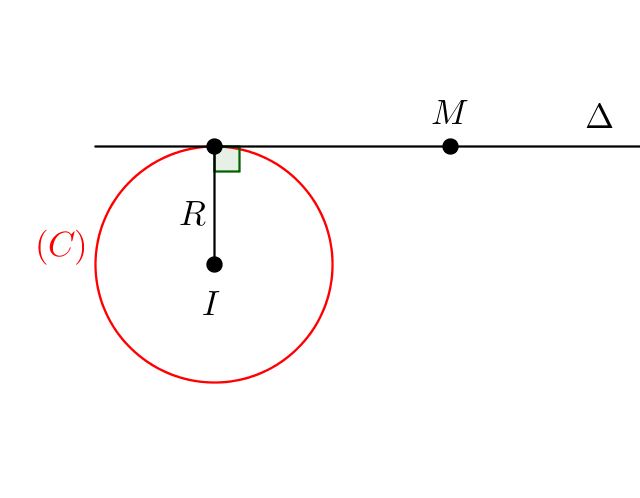
Ý nghĩa hình học của đạo hàm: Đạo hàm của hàm số y = f(x) tại điểm x0 là hệ số góc m tiếp tuyến với đồ thị (C) của hàm số tại điểm M (x0, y0).
Khi đó, phương trình tiếp tuyến của (C) tại điểm M (x0, y0) là y = y'(x0 )(x – x0) + y0.
– Trong đó:
- Với x0 là hoành độ tiếp điểm;
- Với y0 = f(x0) là tung độ tiếp điểm;
- Với y’ = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Nguyên tắc chung để lập được phương trình tiếp tuyến là ta phải tìm được hoành độ tiếp điểm x0.

Các dạng bài tập thường gặp của phương trình tiếp tuyến
Dạng 1: Viết phương trình tiếp tuyến tại M0(x0;y0) ∈ (C)
- Tính đạo hàm của hàm số, thay x0 ta được hệ số góc
Áp dụng (*) ta được phương trình tiếp tuyến cần tìm.
Dạng 2: Cho trước hoành độ tiếp điểm x0
– Tính đạo hàm của hàm số, thay x0 ta được hệ số góc.
– Thay x0 vào hàm số ta tìm được tung độ tiếp điểm.
Dạng 3: Cho trước tung độ tiếp điểm y0
– Giải phương trình y0 = f(x0) để tìm x0.
– Tính đạo hàm của hàm số, thay x0 ta được hệ số góc.
Áp dụng (*) ta được phương trình tiếp tuyến cần tìm.
Chú ý: Có bao nhiêu giá trị của x0 thì có bấy nhiêu tiếp tuyến.
Dạng 4: Cho trước hệ số góc của tiếp tuyến k = y’(x0) = f’(x0)
– Tính đạo hàm và giải phương trình k = y’(x0) = f’(x0) để tìm x0
– Thay x0 vào hàm số ta tìm được tung độ tiếp điểm cần tìm.
Chú ý: Có bao nhiêu giá trị của x0 thì có bấy nhiêu tiếp tuyến.
Một số dạng toán thường gặp khác
– Khi giả thiết yêu cầu viết phương trình tiếp tuyến biết tiếp tuyến vuông góc với đường thẳng : y = ax + b thì điều này
<=> y’(x0). a = -1 ⇔ y’(x0) = -1/a
===> Quay về dạng 4.
– Khi giả thiết yêu cầu viết phương trình tiếp tuyến biết tiếp tuyến song song với đường thẳng
y = ax + b thì điều này ⇔ y’(x0) = a… ===> Quay về dạng 4.
– Khi giả thiết yêu cầu viết phương trình tiếp tuyến tại giao điểm với đường thẳng y = ax + b thì việc đầu tiên là tìm tọa độ giao điểm của (C) và đường thẳng… ===> Quay về dạng 1
Chú ý:
Cho hai đường thẳng d1: y = a1x + b1 với a1 là hệ số góc của đường thẳng d1 và y = a2x + b2 với a2 là hệ số góc của đường thẳng d2.
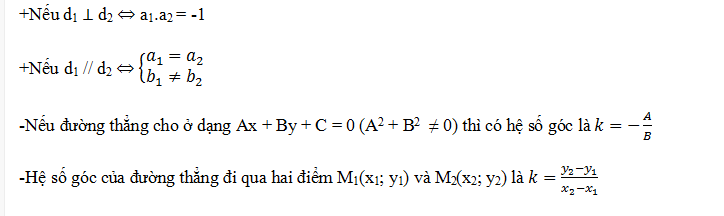
Bài tập minh họa cách giải bài toán phương trình


Cám ơn bạn đã theo dõi bài viết này của chúng tôi, hẹn gặp lại bạn ở những bài viết khác !





