Tính chất của hai tiếp tuyến cắt nhau có những tính chất nào ? Cùng chúng tôi khám phá ngay những nội dung cần nhớ trong chủ đề này nhé.
Tham khảo bài viết khác:
Tính chất của hai tiếp tuyến cắt nhau
Tóm tắt nội dung
– Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm
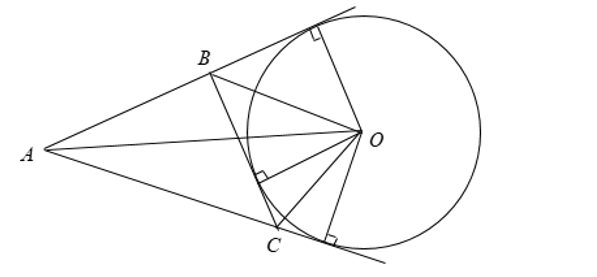
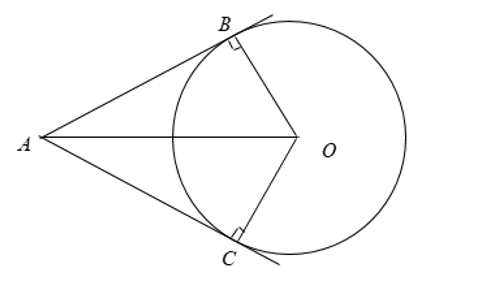
===> Nghĩa là cho đường tròn (O), B, C ∈ (O). Tiếp tuyến của (O) tại B, C cắt nhau tại A
======> Khi đó:
+) AB = AC
+) Tia OA là phân giác của góc BOC ( Hay góc OAB = góc OAC )
+) Tia AO là phân giác của góc BAC ( Hay góc AOB = góc AOC )
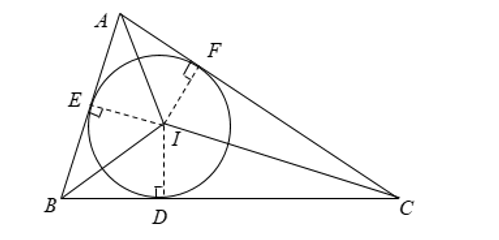
Đường tròn nội tiếp của tam giác.
– Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, còn tam giác gọi là ngoại tiếp đường tròn, khi đó tam giác đó gọi là tam giác ngoại tiếp đường tròn.
– Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác
Đường tròn bàng tiếp tam giác.
– Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.
– Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, giao điểm này cùng nằm trên đường phân giác góc A.
==> Với một tam giác, có ba đường tròn bàng tiếp.
Cám ơn bạn đã theo dõi bài viết của chúng tôi, hy vọng sau khi đọc xong bài viết này bạn sẽ hiểu hơn về chủ đề này nhé !