Vị trí tương đối của đường thẳng và đường tròn trong bài viết này sẽ có những nội dung nào được chia sẻ đến bạn. Cùng chúng tôi khám phá ngay nội dung bài viết dưới đây nhé !
Tham khảo bài viết khác:
Vị trí tương đối của đường thẳng và đường tròn
Tóm tắt nội dung
– Cho đường tròn (O;R) và một đường thẳng Δ bất kì. Gọi d là khoảng cách từ tâm O của đường tròn đến đường thẳng đó.
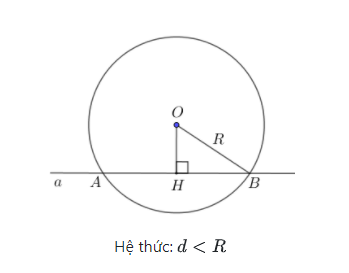
1. Đường thẳng Δ và đường tròn ( O;R ) cắt nhau.
==> Khi đó đường thẳng và đường tròn có hai điểm chung và khoảng cách d = OH < R
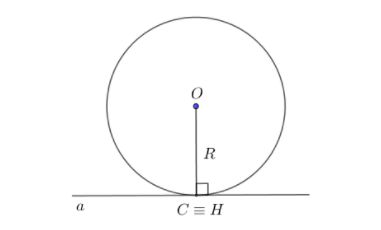
2. Đường thẳng Δ và đường tròn (O;R) tiếp xúc với nhau.
==> Khi đó đường thẳng và đường tròn có một điểm chung và khoảng cách d = OC = R.
==> Đường thẳng Δ được gọi là tiếp tuyến của đường tròn và điểm C là tiếp điểm.
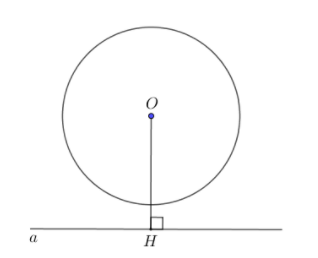
3. Đường thẳng Δ và đường tròn (O;R) không giao nhau.
==> Khi đó đường thẳng và đường tròn không có điểm chung và khoảng cách d = OH > R
Hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn
1. Đường thẳng và đường tròn cắt nhau
+) Số điểm chung: 2
+) Hệ thức giữa d và R: d < R
2. Đường thẳng và đường tròn tiếp xúc nhau
+) Số điểm chung: 1
+) Hệ thức giữa d và R: d = R
3. Đường thẳng và đường tròn không giao nhau
+) Số điểm chung: 0
+) Hệ thức giữa d và R: d > R
Bài tập minh họa
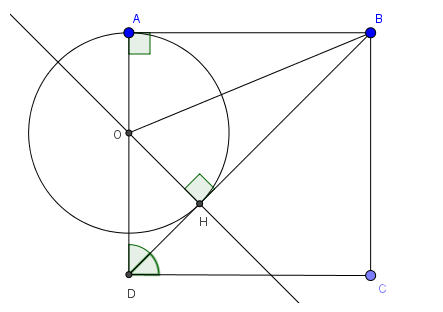
Bài tập 1: Cho hình vuông ABCD. Trên đường chéo BD lấy điểm H sao cho BH = BA , qua H vẽ đường thẳng vuông góc với BD cắt AD tại O
a) So sánh OA, OH và HD
b) Xác định vị trí tương đối của BD với (O; OA)
– Hướng dẫn giải:
Cám ơn bạn đã theo dõi bài viết của chúng tôi, hy vọng bài viết sẽ đem đến cho bạn những nội dung hay và hữu ích nhất nhé !