Trọng tâm của tam giác là gì ? Dưới bài viết này của chúng tôi sẽ chia sẻ đến bạn tất tần tật những thông tin xoay quanh trọng tâm, cũng như từng trường hợp trọng tâm trong các kiểu tam giác
Cùng theo dõi ngay bài viết nhé !
Tham khảo bài viết khác:
Trọng tâm của tam giác là gì ?
Tóm tắt nội dung
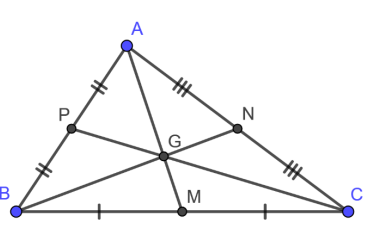
– Trọng tâm của tam giác là giao điểm của 3 đường trung tuyến.
( Đường trung tuyến của một tam giác là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện )
– Ví dụ minh họa:

+) Tam giác ABC với AM, BN, CP lần lượt là 3 đường trung tuyến xuất phát từ 3 đỉnh A, B, C. Điểm G là giao điểm của 3 đường trung tuyến và được gọi là trọng tâm của tam giác ABC
Trọng tâm của tam giác có tính chất gì ?
– Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
– Tam giác ABC, với các đường trung tuyến AM, BN, CP và trọng tâm G, ta có:
- GA = 2/3 AM
- GC = 2/3 GP
- BG = 2/3 GN
Cách xác định trọng tâm tam giác
– Cách 1:
+) Tìm trung điểm M của BC sao cho MC = MB
+) Nối A với M ta được đường trung tuyến AM.
+) Tương tự với các đường trung tuyến còn lại.
+) Giao 3 đường trung tuyến là điểm G. Suy ra G chính là trọng tâm tam giác ABC.

– Cách 2:
+) Tìm trung điểm M của BC sao cho MC = MB
+) Nối A với M ta được đường trung tuyến AM.
+) Trên đoạn thẳng AM lấy điểm G sao cho: AG = 2/3 AM
+) Vậy theo tính chất trọng tâm ta có G chính là trọng tâm tam giác ABC.
==> Cho tam giác ABC có AM, BN, CP lần lượt là ba đường trung tuyến tại đỉnh A, B, C. Ta có giao của ba đường trung tuyến là điểm G. Vậy G là trọng tâm của tam giác ABC.
Trọng tâm của tam giác vuông
– Trọng tâm của tam giác vuông cũng được xác định giống như trọng tâm của tam giác thường.
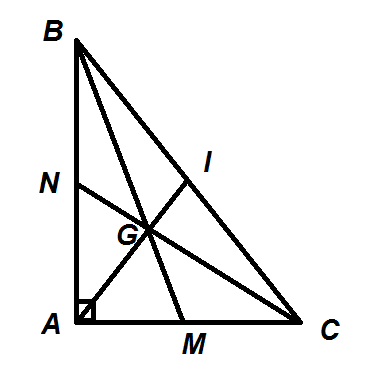
– Tam giác ABC vuông tại A
==> 3 đường trung tuyến AI, BM, CN giao nhau tại trọng tâm G. Ta có AI là trung tuyến của góc vuông BAC nên AI = 1/2 BC = IB = IC.
Trọng tâm của tam giác đều
– Tam giác ABC đều, G là giao điểm ba đường trung tuyến, đường cao, đường phân giác.
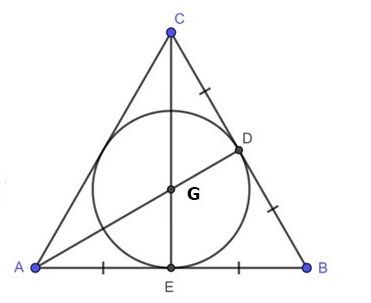
==> Vì vậy theo tính chất của tam giác đều ta có G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.
Trọng tâm của tam giác cân
– Trọng tâm của một tam giác cân cũng được xác định giống tam giác thường.
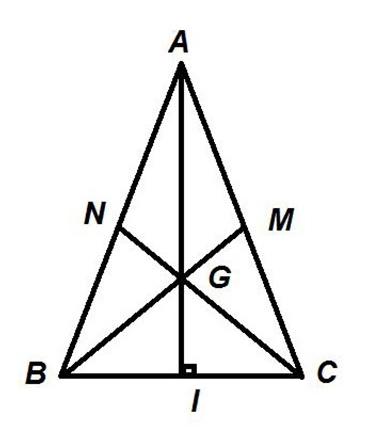
– Xét tam giác ABC cân tại A với G là trọng tâm. Khi đó, AG vừa là đường trung tuyến, vừa là đường phân giác và là đường cao của tam giác ABC này.
==> Ta có: AG vuông góc với BC. Suy ra, tam giác ACI và ABI lần lượt vuông tại I.
Trọng tâm của tam giác vuông cân
– Có tam giác ABC vuông cân tại A và G là trọng tâm. AI là đường trung trực, đường trung tuyến và đường cao của tam giác này nên AI vuông góc với BC.
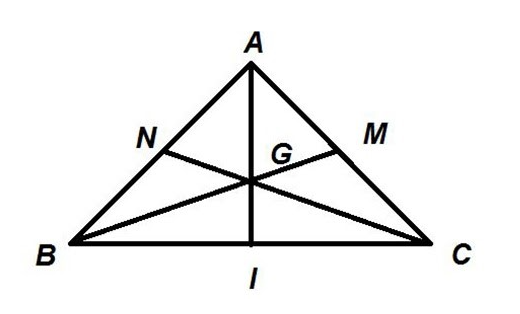
– Mặt khác, vì tam giác ABC vuông cân tại A nên:
AB = AC.
=> BM = CN và BN = AN = CM = AM.
Cám ơn bạn đã theo dõi những nội dung của Đồng Hành Cho Cuộc Sống Tốt Đẹp, hy vọng bài viết sẽ chia sẻ đến bạn nhiều thông tin hữu ích nhất !!!





