Tứ giác nội tiếp đường tròn là gì ? Những định lý, tính chất, dấu diệu nhận biết cũng như cách chứng minh tứ giác nội tiếp là gì ? Cùng chúng tôi tìm hiểu ngay dưới bài viết này nhé !
Tham khảo bài viết khác:
Lý thuyết Tứ giác nội tiếp đường tròn
Tóm tắt nội dung
1. Khái niệm
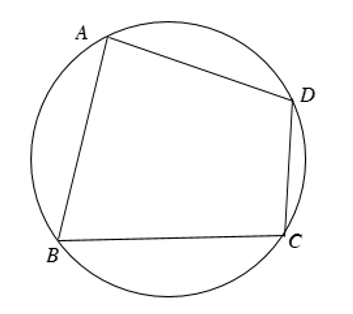
– Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn ( gọi tắt là tứ giác nội tiếp )
2. Định lý
+) Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.
+) Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.
Tứ giác ABCD nội tiếp đường tròn (O), suy ra góc A + B + C + D = 180°
Dấu hiệu nhận biết tứ giác nội tiếp
+) Tứ giác có tổng hai góc đối bằng 180°.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
+) Tứ giác có bốn đỉnh cách đều một điểm ( mà ta có thể xác định được ). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.
+) Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.
Lưu ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.
Những cách chứng minh tứ giác nội tiếp đường tròn
– Dưới đây là 6 cách chứng minh tứ giác nội tiếp đường tròn:
- Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
- Chứng minh tứ giác có tổng 2 góc đối bằng 180°
- Chứng minh từ hai đỉnh
- Tứ giác có tổng số đo hai góc đối bằng nhau
- Chứng minh qua góc ngoài của tứ giác
- Chứng minh bằng phương pháp phản chứng
Bài tập minh họa
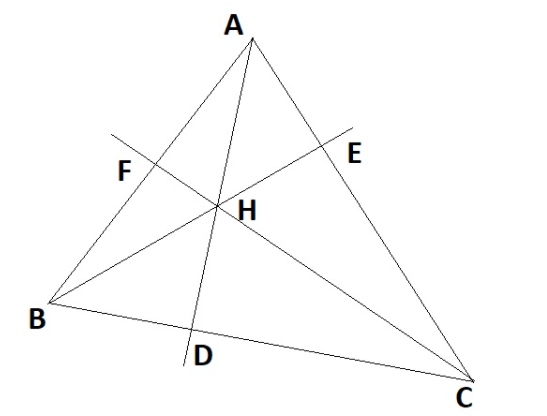
Bài tập 1: Cho ΔABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng:
a) Tứ giác BCEF nội tiếp.
b) HA.HD = HB.HE = HC.HF
– Hướng dẫn giải:
a) Ta có ˆBEC = ˆBFC = 90°.
Suy ra tứ giác BCEF nội tiếp đường tròn có đường kính BC.
b) Gọi O là trung điểm của BC, vẽ đường tròn tâm O, đường kính BC. Xét ΔBHF và ΔCHE có:
ˆFHB = ˆEHC ( đối đỉnh ).
ˆEBF = ˆECF (hai góc nội tiếp cùng chắn).
Suy ra ΔBHF ∼ ΔCHE
BH/CH = HF/HE hay HB.HE = HC.HF (1).
Chứng minh tương tự đối với ΔAHE và ΔBHD, ta có: HA.HD = HB.HE (2).
Từ (1) và (2) suy ra: HA.HD = HB.HE = HC.HF ( đpcm).
Với những nội dung trong bài, chúng tôi hy vọng sẽ đem đến những kiến thức hữu ích nhất đến bạn !