Chia đa thức cho đơn thức gồm những lý thuyết và những dạng bài tập nào thường gặp. Hãy theo dõi những nội dung dưới bài viết này để hiểu hơn về chủ đề này nhé !
Tham khảo bài viết khác:
Chia đa thức cho đơn thức
Tóm tắt nội dung
– Muốn chia đa thức A cho đơn thức B (trường hợp các hạng tử của đa thức A đều chia hết cho đơn thức B), ta chia mỗi hạng tử của A cho B rồi cộng các kết quả với nhau.
Chú ý: Trường hợp đa thức A có thể phân tích thành nhân tử, thường ta phân tích trước để rút gọn cho nhanh.

Các dạng bài tập trong chia đa thức cho đơn thức
Dạng 1: Thực hiện phép tính và rút gọn biểu thức
Bài tập 1: Không làm tính chia, hãy xét xem đa thức A có chia hết đơn thức B không:
A = 15xy^2 + 17xy^3 + 18y^2 B = 6y^2
– Hướng dẫn giải:
Nhận thấy:
15xy^2 chia hết cho 6y^2
17xy^3 chia hết cho 6y^2
18y^2 chia hết cho 6y^2
Vậy A = 15xy^2 + 17xy^3 + 18y^2 chia hết cho 6y^2 hay A chia hết cho B.
Bài tập 2: Làm phép tính chia
![]()
( Gợi ý : Có thể đặt x – y = z rồi áp dụng qui tắc chia đa thức cho đơn thức )
– Hướng dẫn giải:
Dạng 2: Tính giá trị của biểu thức tại x = x0
– Phương pháp giải:
Thay x = x0 vào biểu thức rồi thực hiện phép tính.
Nếu biểu thức có nhiều biến thì ta thay lần lượt từng biến theo giả thiết.
– Bài tập 3: Tính giá trị biểu thức A = (x^2y+y^2x) : xy tại x=1; y=1
– Hướng dẫn giải:
Ta có:
A = (x^2y + y^2x) : xy
= x^2y : xy + y^2x : xy = x + y
Với x=1; y=1 ta có: A = x+y = 1+1 = 2
Dạng 3: Tìm m để phép tính chia cho trước là phép chia hết.
– Phương pháp giải:
+) Sử dụng nhận xét: Đa thức A chia hết cho đơn thức B nếu các hạng tử của đa thức A đều chia hết cho đơn thức B.
+) Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ nhỏ hơn hoặc bằng số mũ của nó trong A
Bài tập 4: Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B:
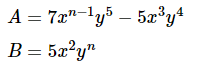
– Hướng dẫn giải:
Cám ơn bạn đã theo dõi nội dung bài viết của chúng tôi, hy vọng bài viết sẽ đem đến cho những nội dung hữu ích nhất !