Đối xứng trục là gì ? Hình như thế nào sẽ có trục đối xứng ? Cùng chúng tôi đi định nghĩa và giải đáp những thắc mắc dưới nội dung bài viết này nhé !
Tham khảo bài viết khác:
Đối xứng trục là gì ?
Tóm tắt nội dung
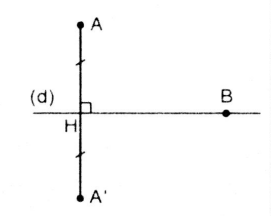
1. Hai điểm đối xứng qua một đường thẳng
– Định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
==> Quy ước: Nếu điểm B nằm trên đường thẳng d thì điểm đối xứng của B qua đường thẳng d cũng chính là điểm B.
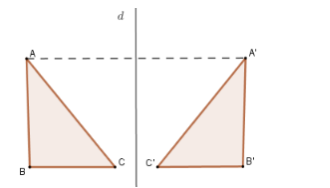
2. Hai hình đối xứng qua đường thẳng
– Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại.
Đường thẳng d gọi là trục đối xứng của hai hình đó.

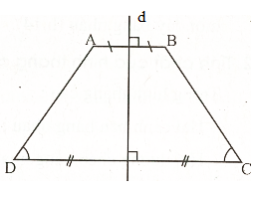
Hình có trục đối xứng là hình như thế nào ?
– Định nghĩa: Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.
==> Ta nói rằng hình H có trục đối xứng.
– Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
==> Đường thẳng d là trục đối xứng của hình thang cân ABCD.
Bài tập ví dụ minh họa có đáp án chi tiết
Ví dụ minh họa: Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng:
a) D đối xứng với E qua AH.
b) Δ ADC đối xứng với Δ AEB qua AH.
– Hướng dẫn giải:
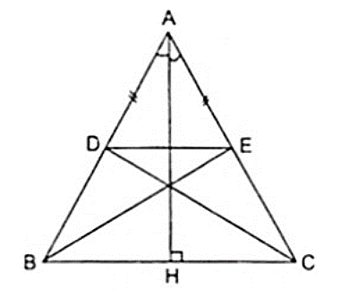
a) Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
⇒ D đối xứng với E qua AH.
b) Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.
⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.
Mặt khác, ta có A đối xứng với A qua AH theo quy ước.
⇒ Δ ADC đối xứng với Δ AEB qua AH.
Cám ơn bạn đã theo dõi bài viết đối xứng trục là gì của chúng tôi, hẹn gặp lại bạn ở những nội dung bài viết tiếp theo trên trang web donghanhchocuocsongtotdep.vn nhé !