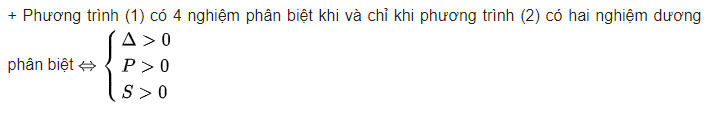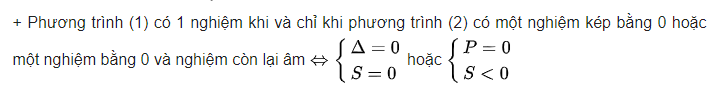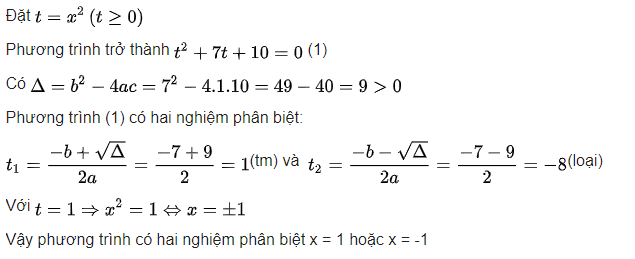Phương trình trùng phương là gì ? Trong dạng phương trình này chúng ta sẽ đi tìm nghiệm, biện luận số nghiệm như thế nào ? Hãy cùng chúng tôi theo dõi những thông tin dưới bài viết này nhé !
Tham khảo bài viết khác:
Phương trình trùng phương là gì ?
Tóm tắt nội dung
1. Khái niệm về phương trình trùng phương
– Phương trình trùng phương theo định nghĩa là phương trình bậc 4 có dạng: ax^4 + bx^2 + c = 0 (a ≠ 0)
2. Cách giải phương trình trùng phương
– Cho phương trình ax^4 + bx^2 + c = 0 (a ≠ 0) (1)
+) Bước 1: Đặt x^2 = t (ĐK t ≥ 0), ta được phương trình bậc hai ẩn t: at^2 + bt + c = 0 (a ≠ 0) (2)
+) Bước 2: Giải phương trình bậc hai ẩn t.
+) Bước 3: Giải phương trình x^2 = t để tìm nghiệm .
+)Bước 4: Kết luận.

3. Biện luận số nghiệm của phương trình trùng phương
+) Phương trình (1) có 4 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm dương phân biệt.
+) Phương trình (1) có 3 nghiệm phân biệt ⇒ phương trình (2) có 1 nghiệm dương và một nghiệm t = 0.
+) Phương trình (1) có 2 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm trái dấu hoặc có nghiệm kép dương.
+) Phương trình (1) có duy nhất 1 nghiệm ⇒ phương trình (2) có nghiệm kép x = 0 hoặc có một nghiệm x = 0 và một nghiệm âm.
+) Phương trình (1) vô nghiệm ⇒ phương trình (2) vô nghiệm hoặc có hai nghiệm âm.
Bài tập minh họa
Bài tập 1: Giải phương trình sau: X^4 + 7X^2 + 10
– Hướng dẫn giải:
Bài tập 2: Giải và biện luận theo m số nghiệm của phương trình: ( m – 2 )x^4 + 3x^2 – 1
– Hướng dẫn giải:
Với m + 2 = 0 ⟺ m = – 2, phương trình đã cho trở thành:
Có P khác 0 nên phương trình không có nghiệm bằng 0 nên phương trình (1) không có 3 nghiệm phân biệt hoặc 1 nghiệm
Phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt
Hy vọng những nội dung chúng tôi chia sẻ đến bạn trong bài viết sẽ đem đến những thông tin hữu ích nhất cho bạn. Cám ơn và hẹn gặp lại ở những bài viết tiếp theo nhé !